Basics of Statistical Mechanics¶

Phase Space¶

Why are statistics important? In statistical physics, we are in fact dealing with DoFs in the order of Avogadro’s number, most of the time. If we are going to calculate the dynamics of these systems by combining all the dynamics of each particles, it becomes rather difficult. It already takes a huge amount of storage to store one screenshot of the system. Assuming each DoF take only 8 bits, we need \(10^23\) bytes that is \(10^17\) GB. It seems to be impossible to store this one snapshot of the system. It is time to steer away from this Newtonian approach.

Fig. 8 Newton’s plan of mechanics. Mechanics was in the center of all physics.

What is mechanics? Mechanics is the thinking that deals with dynamics of object in the following way:

Description of initial state;
Time evolution of the system;
Extraction of observables.

The initial state of an object is exactly what the name indicates. In a coordinate system approach, the initial state should include the coordinates and the time derivative of the coordinates since we are interested in dynamics. In fact, the coordinates and time derivative of them form a phase space. In general, a vector in phase space is a complete description of the state of an object. Thus time evolution of the object is simply the motion of state vector in phase space. Finally, we will do whatever is needed to extract observables. For example, we could trivially use the projection of points in phase space to get the position or velocity.

The problem arise when it comes to a system with a large amount of particles. As mentioned previously, it’s in general not possible to record all these DoFs. We need a completely new scheme.

Boltzmann Factor¶

\[\text{probability of a point in phase space} = \exp(-\frac{E}{k_B T})\]

Boltzmann factor gives us the (not normalized) probability of the system staying on a phase space state with energy \(E\).

Why Boltzmann Factor

Why does Boltzmann factor appear a lot in equilibrium statistical mechanics? Equilibrium of the system means when we add infinitesimal amount of energy to the whole thing including system and reservoir, a characteristic quantity \(C(E) = C_S C_R\) won’t change. That is the system and the reservoir will have the same changing rate of the characteristic quantity when energy is changed, i.e.,

\[\frac{\partial \ln C_S}{\partial E_S} = - \frac{\partial \ln C_R}{\partial E_R} .\]

We have \(\mathrm dE_1 = -\mathrm dE_2\) in a equilibrium state. They should both be a constant, which we set to \(\beta\). Finally we have something like

\[\frac{\partial \ln C_S}{\partial E_S} = \beta\]

which will give us a Boltzmann factor there.

This is just a very simple procedure to show that Boltzmann factor is kind of a natural factor in equilibrium system.

Partition Function¶

For a given Hamiltonian H, the (classical) partition function Z is

\[Z = \int d p \int d x e^{-\beta H}\]

A simple example is the Harmonic Oscillator,

\[H = \frac{p^2}{2m} + \frac{1}{2} q x^2\]

The partition function

\[Z = \int e^{-\beta p^2/(2m)} d q \int e^{-\beta \frac{1}{2} q x^2 } d x = 2\pi \sqrt{m/q} \frac{1}{\beta}\]

Energy

\[E = \frac{1}{Z} \int \int e^{-\beta p^2/(2m)} e^{-\beta \frac{1}{2} q x^2 } H d p d x = \cdots = k_B T\]

(This result is obvious if we think about equipartition theorem.)

A more clever approach for the energy is to take the derivative of partition function over \(\beta\), which exactly is

\[\langle E \rangle = -\frac{\partial }{\partial \beta } \ln Z\]

In our simple case,

\[\ln Z = -\frac{\partial}{\partial \beta} \left(\ln (k_B T) + \mathrm{Some Constant} \right)= k_B T\]

This is the power of partition function. To continue the SHO example, we find the specific heat is

\[C = k_B\]

Does This Result Depend on SHO

This result has nothing to do with the detail of the SHO, no matter what mass they have, no matter what potential constant \(q\) they have, no matter what kind of initial state they have. All the characteristic quantities of SHO are irrelevant. Why? Mathematically, it’s because we have Gaussian integral here. But what is the physics behind this? Basicly this classical limit is a high temperature limit.

Magnetization¶

We have such a result in an experiment of magnetization with N magnetic dipoles in 1D.

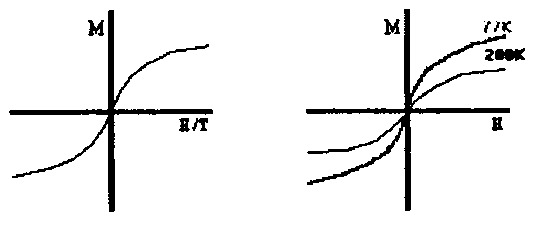
How can we describe this with a theory?

It’s not possible to describe the system by writing down the dynamics of each magnetic dipole. So we have to try some macroscpic view of the system. Probability theory is a great tool for this. The probability of a dipole on a energy state \(E_i\) is

\[P(E_i) = \frac{\exp(-\beta E_i)}{\sum_{i=1}^{n} \exp(-\beta E_i)} .\]

So the megnetization in this simple case is

\[M = (\mu N e^{\beta \mu B} - \mu N e^{-\beta \mu B})/(\exp(\beta \mu B) + \exp(-\beta \mu B)) = \mu N \tanh (\beta \mu B)\]

Python Code

Use ipython notebook to display this result. The original notebook can be downloaded from here. (Just put the link to nbviewer and everyone can view online.)

%pylab inline
from pylab import *

Populating the interactive namespace from numpy and matplotlib

x=linspace(0,10,100)
y=tanh(x)

figure()
plot(x, y, 'r')
xlabel('External Magnetic Field')
ylabel('M')
title('Tanh theory')
show();

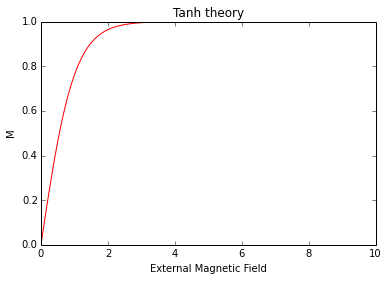
This is exactly the thing we saw in the experiment.

This can be classified as a category of problems. In this specific example we see saturation of magnetization. However this is not alway true.

Examples

Examples can be shown here.

Heat Capacity¶

Another category of problems is temperature related. For example, a study of average energy with change temperature.

For the paramagnetic example, the energy of the system is

\[E = -(\mu B N e^{\beta \mu B} - \mu N e^{-\beta \mu B})/(\exp(\beta \mu B) + \exp(-\beta \mu B)) = -\mu N B \tanh (\beta \mu B)\]

Obviously, no phase transition would occur. But if we introduce self interactions between dipoles and go to higher dimensions, it’s possible to find phase transitions.

Specific Heat¶

\[C = \frac{d}{T}\langle E \rangle\]

Check the behavior of specific heat,

Is there a Discontinuity?
Constant?
Blow up?
Converge?

Specific heat can be used for second order phase transition. An simple example of this is Landau theory.

Importance of Dimensions¶

IPython Notebook about heat capacity of systems with different dimensions. .